The Copying Task
The Copying Task is a benchmarking task in NLP.NLP that assesses recurrent models (and other sequential models)' ability to retain information for long sequence lengths.
The idea is to show the model a sequence of letters/characters/whatever, show it a long blank sequence and then have it spit out the original sequence of characters that we actually care about at the end.
In the paper they use a to define the alphabet of letters that we care about:
- The first 8 items are actual letters that we might care about,
- The 9th item is considered 'blank' and just used to pad out the sequence and make it long for tests
- The 10th item is a 'delimiter' character to tell the model to start spitting out the original sequence.

We can define different lengths of sequence that we want to test against - in the paper they use T to represent this value. For example, T=100 means "define a sequence, run 100 blanks through the system, then have it recall the sequence from the beginning".
To set up the test we:
- use the characters from a 0 to 7 to generate a random sequence of characters that needs to be memorised - this sequence is 10 characters long. We sample with replacement which means letters are allowed to repeat.
- Generate T blank characters
- Use the delimiter to signal to the model that it should generate the remaining steps
- Have the model infer the sequence - since the length of the sequence is known, we can halt after the correct number of characters have been outputted and check to make sure that it is correct.
Our sequence would look something like this.
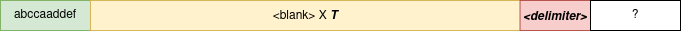
We can trivially generate 1000s of sequences like this and use it as a simple benchmark. We want to train on a diverse set of sequence examples so that the model doesn't over-fit and learn to always predict the same sequence.
As we are sampling with replacement, there are 8^10, or approximately 1.1 Billion possible problems and solutions when the length of the input sequence is 10. As long as we are using relatively small models, it shouldn't be possible for the model to memorise all possible solutions in its weights.
References
Arjovsky, Martin, Amar Shah, and Yoshua Bengio. ‘Unitary Evolution Recurrent Neural Networks’, [pdf]